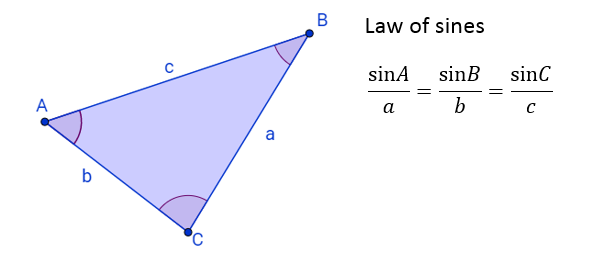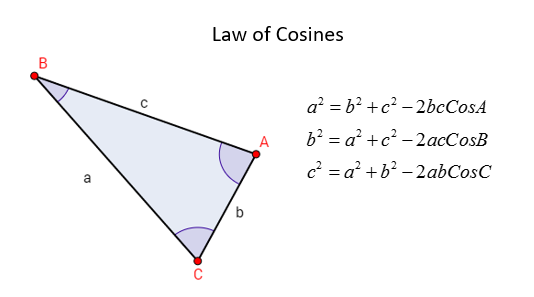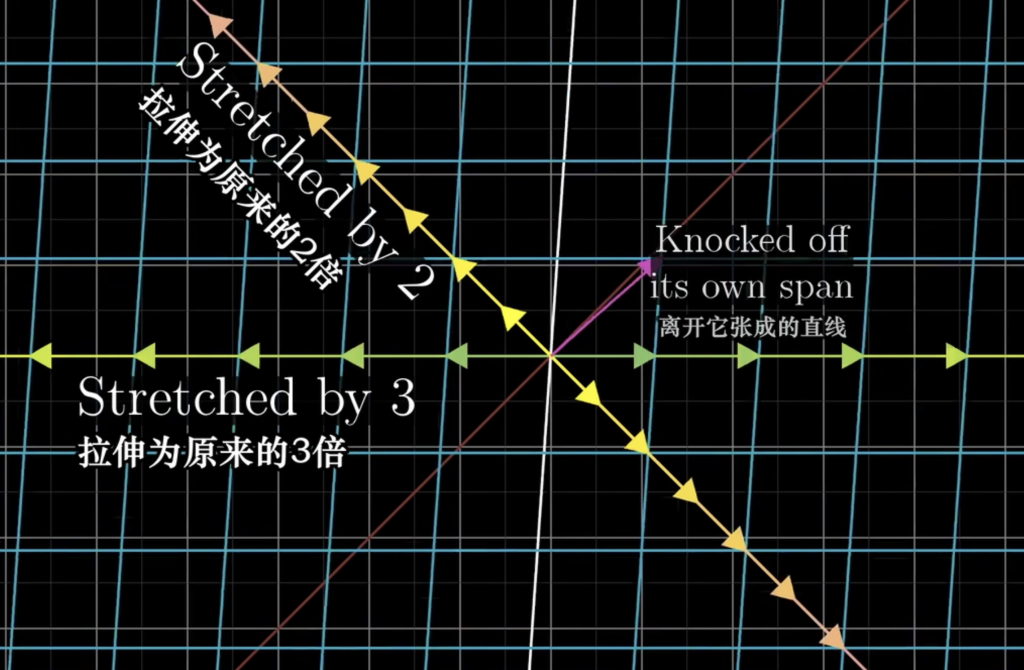
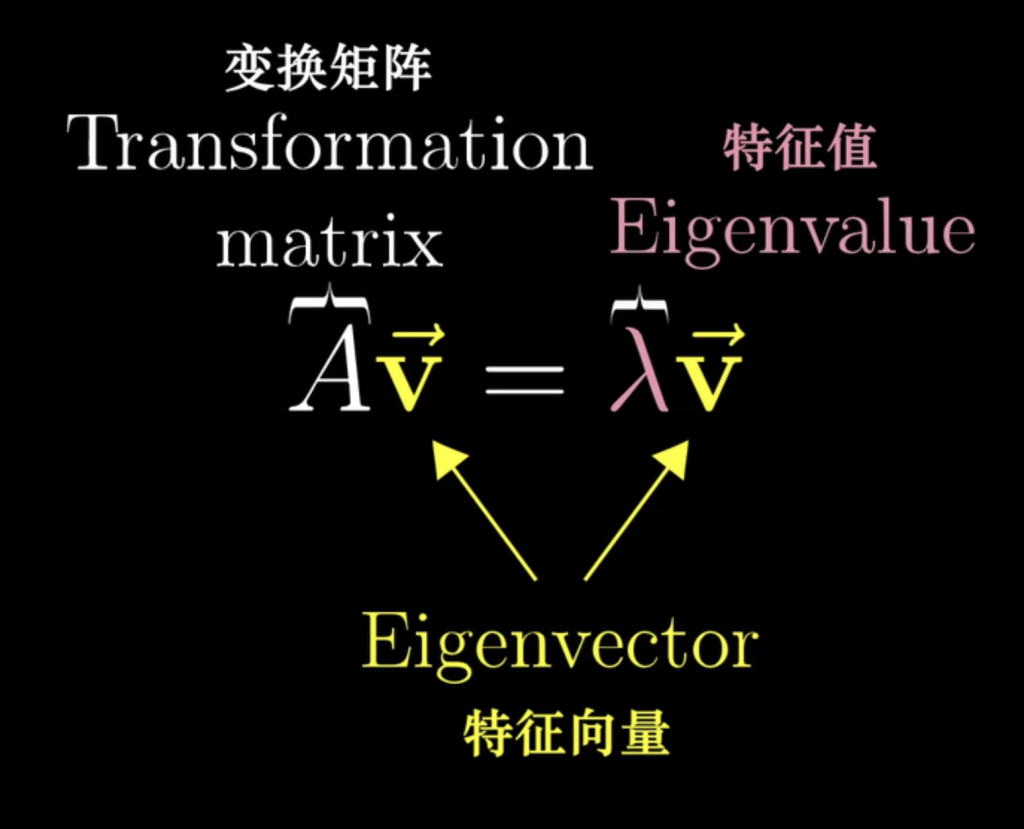
特征向量是变换后不离开其自身所张成直线的向量。特征值即为变换后的缩放倍数。

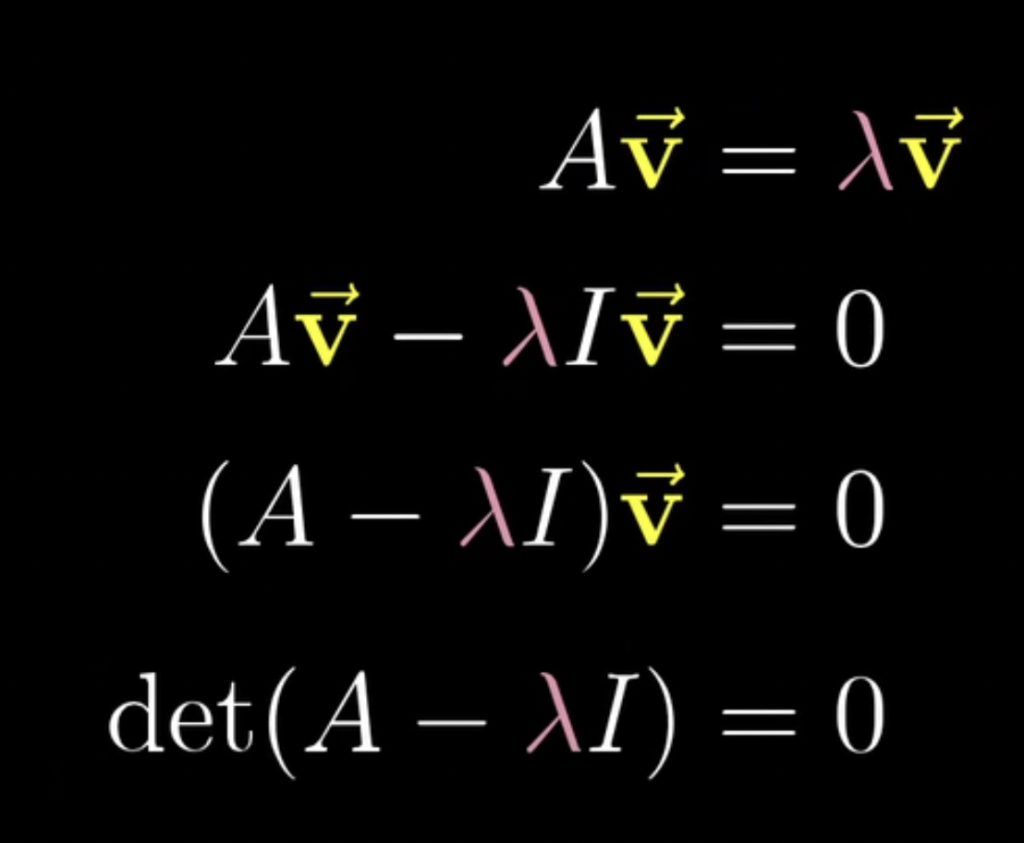

矩阵对角化在力学、电学、人工智能、量子力学等领域均有应用
特征基

www.zhitu.ink 一张图 一句话 解释一个知识点

特征向量是变换后不离开其自身所张成直线的向量。特征值即为变换后的缩放倍数。


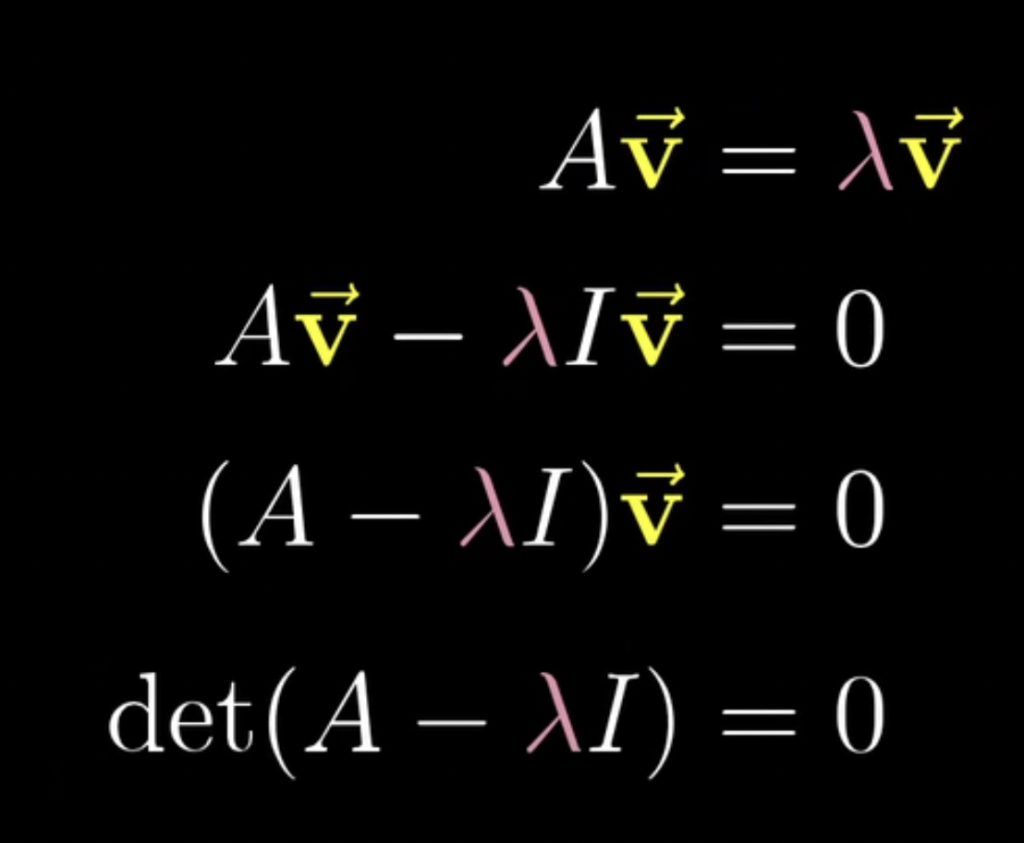

矩阵对角化在力学、电学、人工智能、量子力学等领域均有应用
特征基

当底数是e时,指数函数求导是其本身。因此一般的指数函数常常写成以自然常数e为底数的指数函数(即自然指数函数 natural exponential function),这样能方便计算。
base power exponent logarithm
符号log是由开普勒首次使用的,取logarithm前三个字母。ln中的n代表自然 nature,以自然常数e为底。lg源自拉丁文:logarithmus generalis,表示常用对数(即以10为底的对数)。
幂:1607年,利玛窦和徐光启合译欧几里得的 《几何原本》,在译本中徐光启重新使用了幂字,并有注解:“自乘之数曰幂。”这是中文里首次给如今“幂”这个概念下定义。
指数:推测这里的“指”是取「关键」的意思。因为指数项就像复利的年数一样,对结果影响巨大。
对数:清初随波兰传教士传入,最初是在书中整理的幂和指数「成对」出现的数表,后来就把由幂求指数的运算叫对数了。


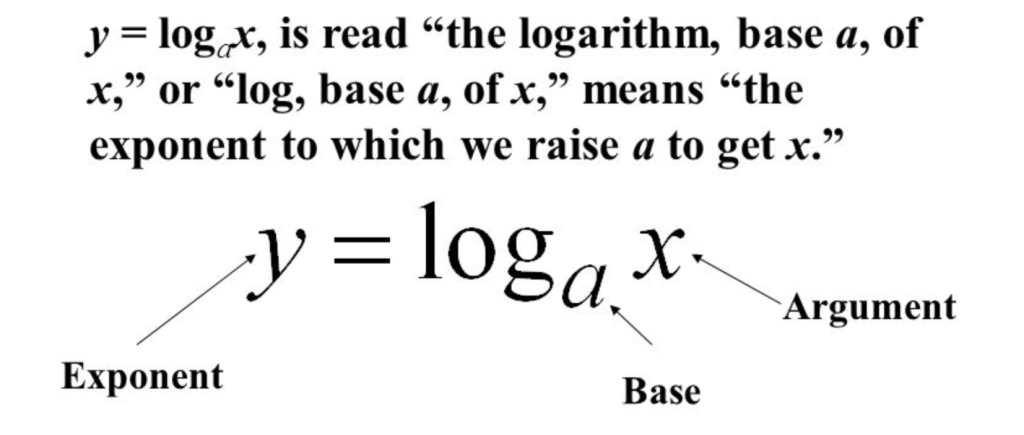
指数函数:指数是自变量,幂是因变量。
对数函数:幂(真数)是自变量,而指数(对数)是因变量, “指数”就是“对数”, 只不过位置不同叫法不同。
幂函数:底数是自变量,幂是因变量。

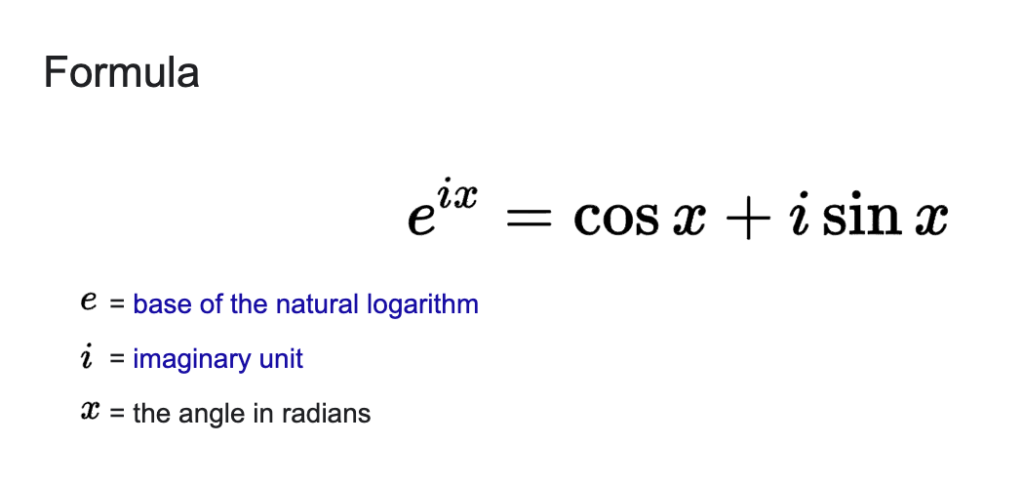
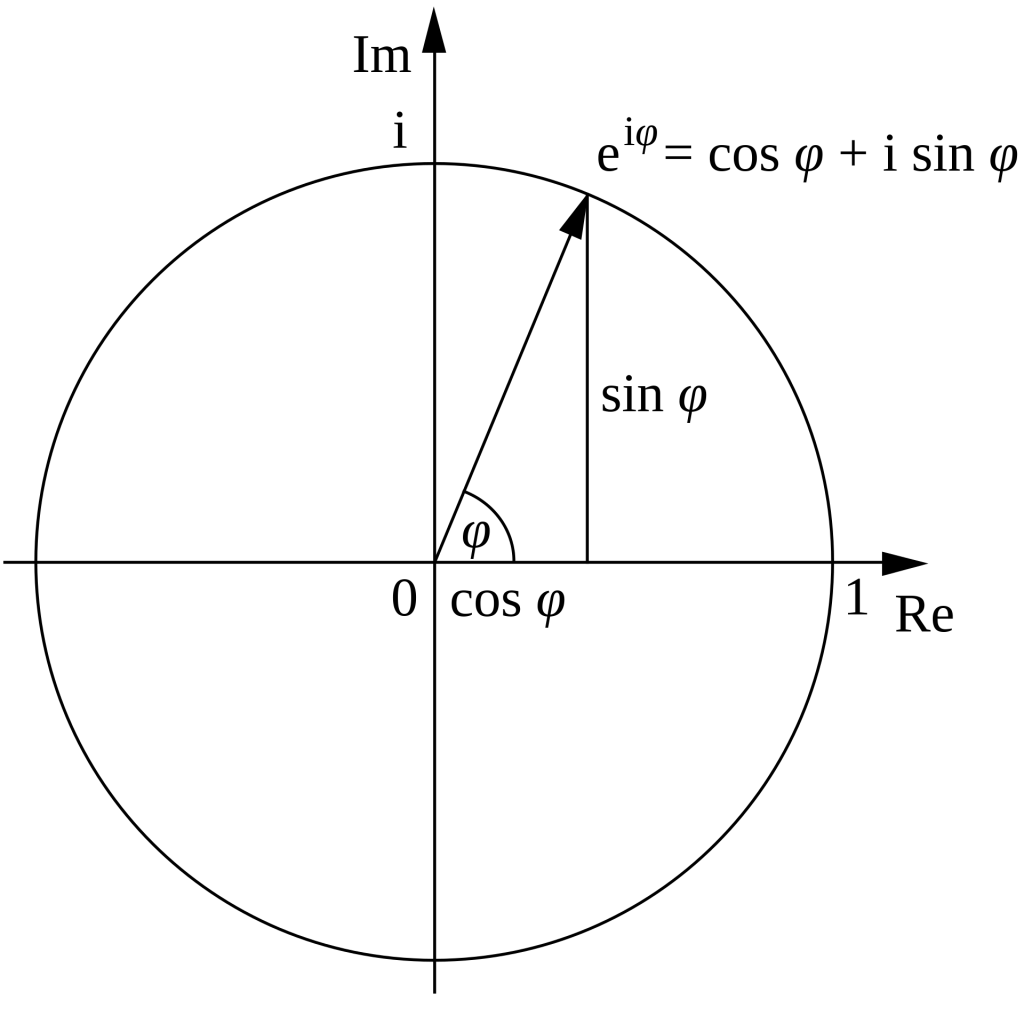
Euler’s identity (欧拉恒等式)

几何学中也有个欧拉公式(在数学历史上有很多公式都是欧拉发现的,它们都叫做欧拉公式,分散在各个数学分支之中。)

欧拉还创造了一批数学符号,如f(x)、Σ、i、e等等,使得数学更容易表述、推广。欧拉还把数学应用到数学以外的很多领域。

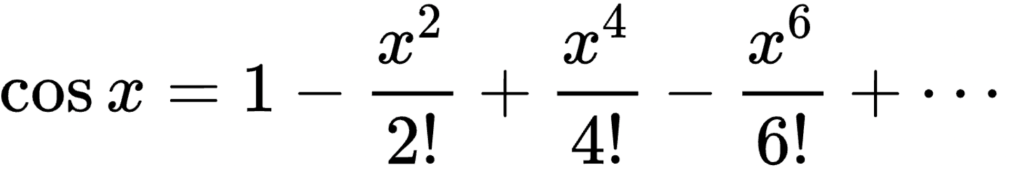
泰勒级数

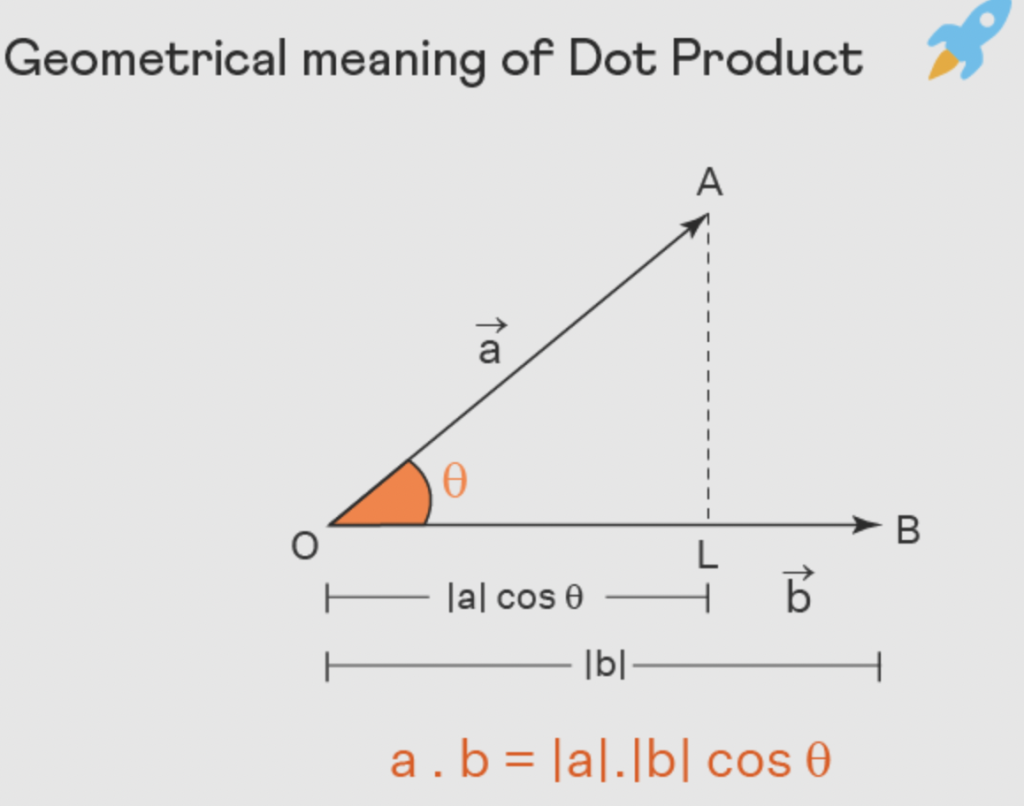
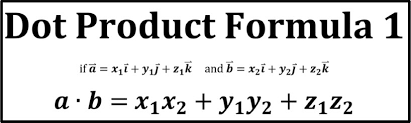

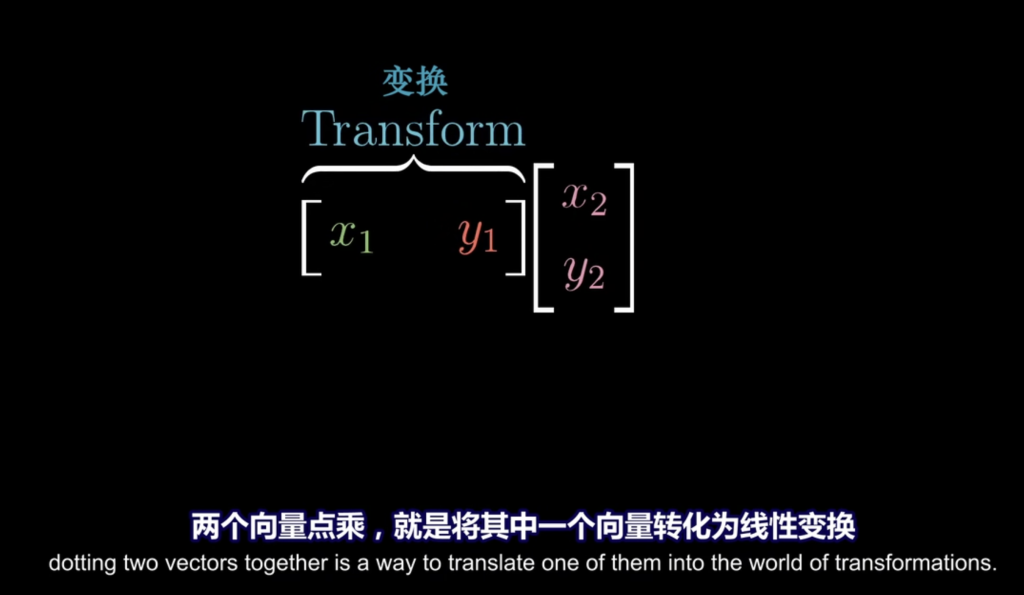
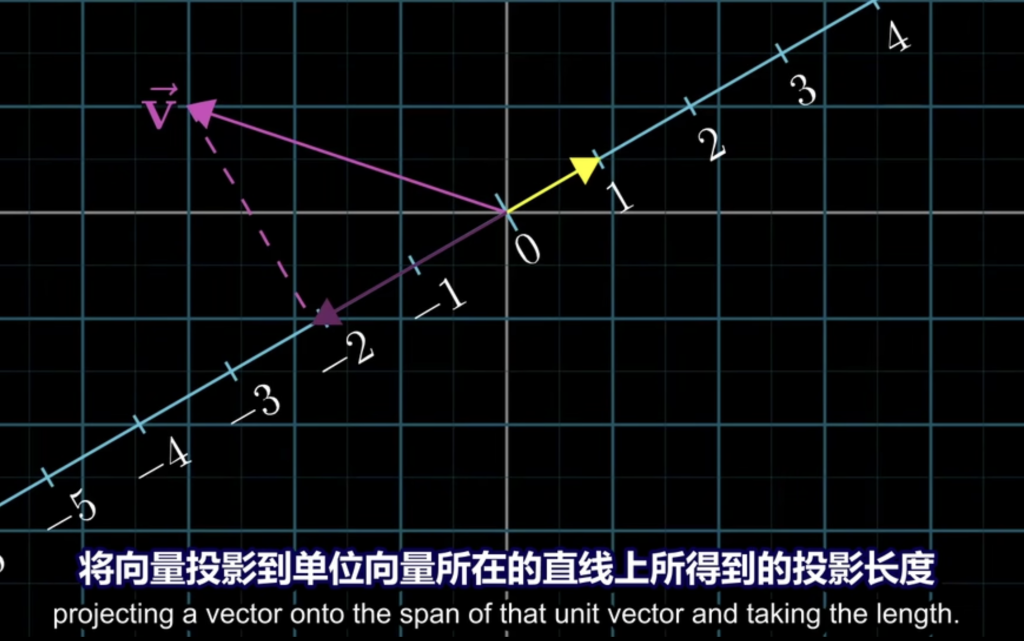
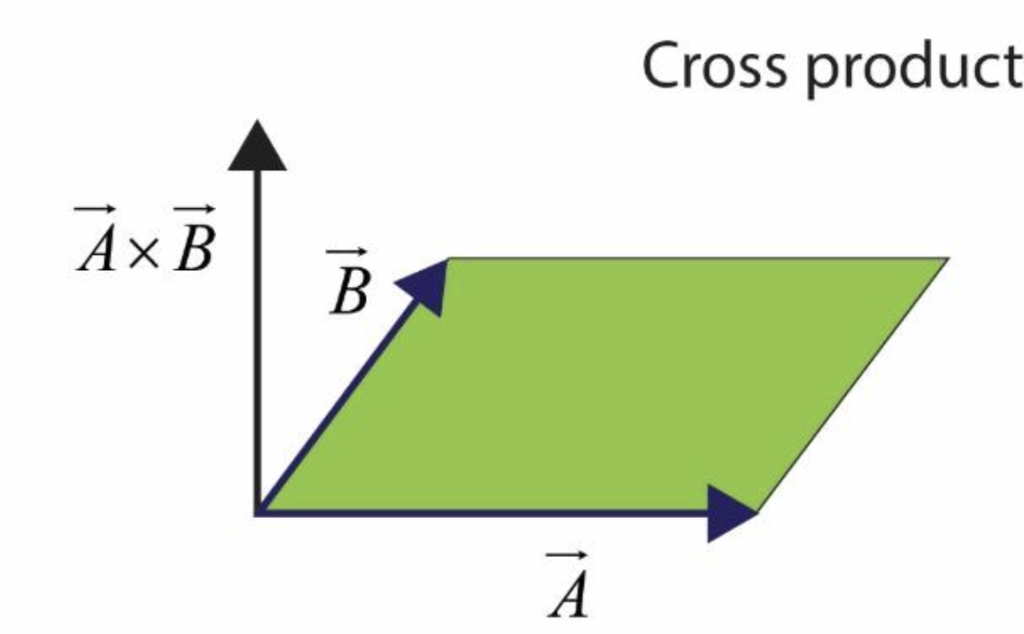
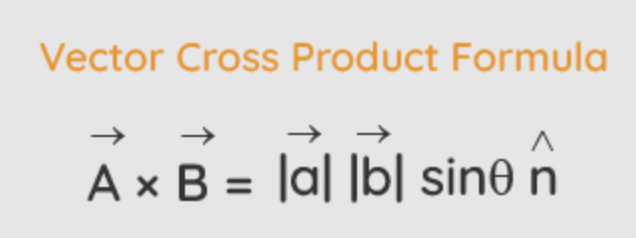
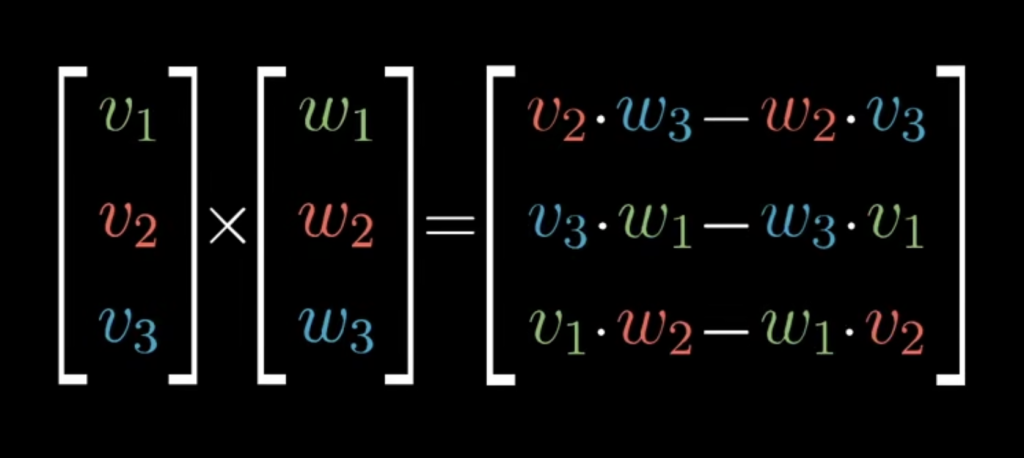
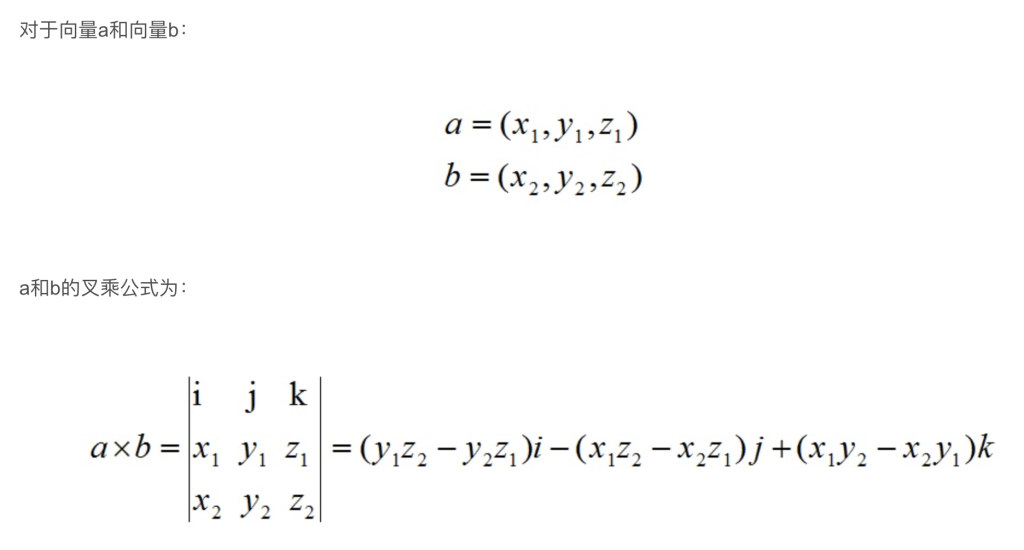

两个向量的叉积同任意向量的点积的结果等于该任意向量与这两个向量所张成的平行六面体的体积。换句话说:将任意随机向量降到1维,使降维后的大小等于该随机向量与两个已知向量所张成的平行六面体的体积 正负号表示是否符合右手定则。该变换的对偶向量就是这两个已知向量的叉积。
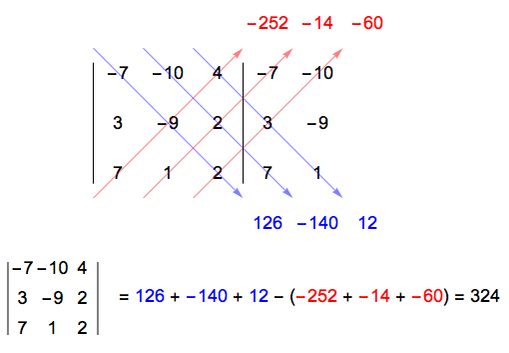
有趣的是 行列式是一个“数”,而函数是一个“式”。
二阶三阶行列式的几何意义:等于列向量所张成的平行四边形/平行六面体的面积/体积,正负号代表了列向量间是否符合右手定则。
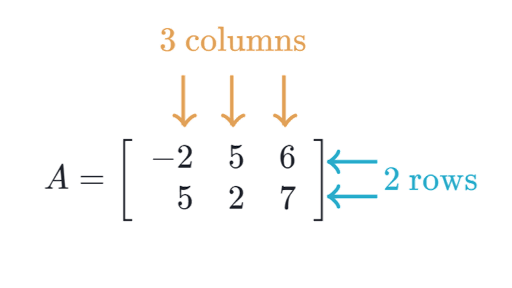
矩阵是一个“阵” 也就是一个数表
代数的“代”意思是代替,即用符号来代替数。而线性代数的“线性”说的是线性空间。
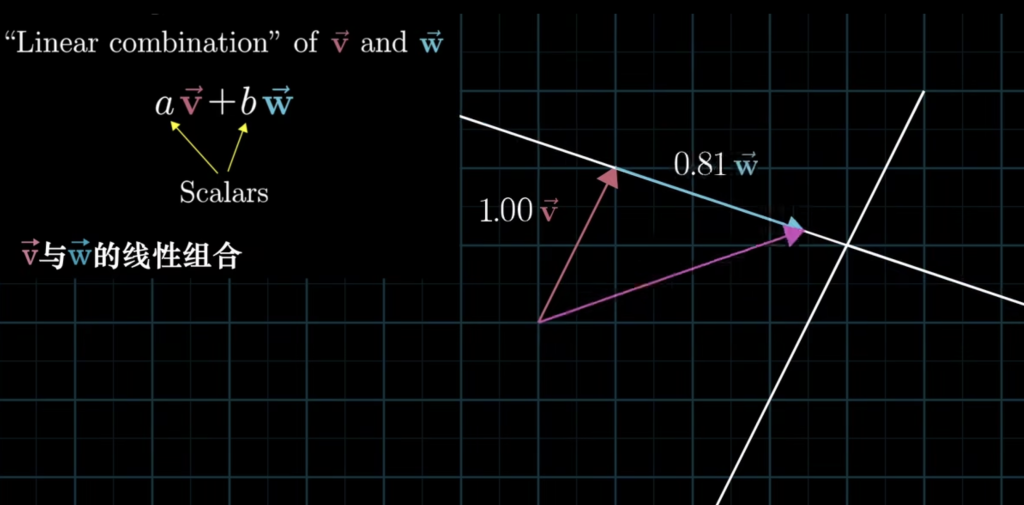
线性代数紧紧围绕向量加法与数乘
线性无关:在二维空间中,两个向量不共线;在三维空间中,三个向量不共面;在n维空间中,有n个向量,其中任意一个向量不能被其他n-1个向量的线性组合来表示,则它们是线性无关的。
行列式的英文determinant源自determine(决定),所以翻译为“判别式”更好一些。那到底是判别什么呢?答:判别的是向量之间的线性关系。行列式为0,那么行/列向量肯定是线性相关的。